2021-0730-MBA-Blast
MBA-Blast: Unveiling and Simplifying Mixed Boolean-Arithmetic Obfuscation
作者:Binbin Liu, Junfu Shen, Jiang Ming, Qilong Zheng, Jing Li, Dongpeng Xu
单位:University of Science and Technology of China, University of New Hampshire, University of Texas at Arlington
会议:USENIX Security 2021
链接:https://www.usenix.org/system/files/sec21fall-liu-binbin.pdf
Introduction
Mixed Boolean-Arithmetic (MBA)作为一种混淆方式,由于开销低、鲁棒性高、使用方便等特点,常在恶意软件及软件加固中被用于保护核心算法。这种混淆技术通过算术运算(ADD、IMUL)及布尔运算(AND、OR、NOT)来替代原来的逻辑运算,以达到混淆的效果。然而目前对抗MBA混淆的方法要么为特定的模式设计,要么在实践中会产生大量错误的结果:pattern matching, bit-blasting, program synthesis。MBA deobfuscation 困难的根本原因在于算术运算与布尔运算的混合使得常规的化简规则无法使用(交换律、结合律、分配律)。
作者研究了MBA混淆的数学原理并证明了MBA设计中隐藏的双向转换特征:作者发现MBA转换在1-bit变量和任意长度整数上的行为相同。根据这一发现,作者设计了MBA-Blast,其能够将MBA表达式有效的化简为简单形式。其核心思想在于将所有bitwise表达式转换成1-bit的特定的MBA形式,然后进行算术规约。当位运算替换完成后,可以使用传统的运算定律进行化简。作者提供了一个数学证明来支撑这一结论。
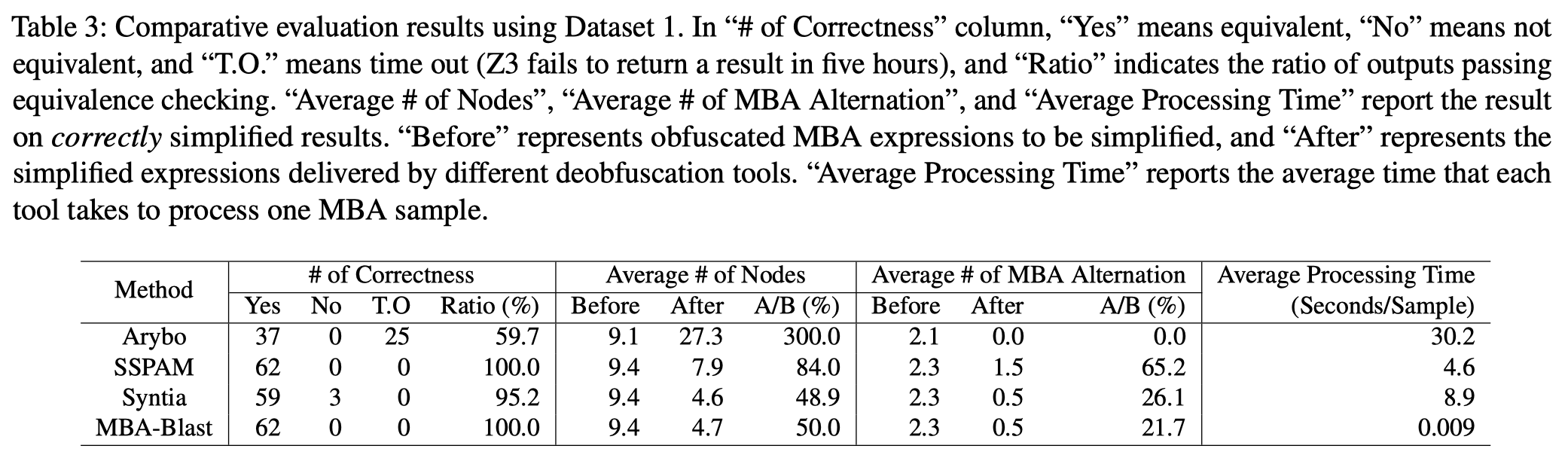
为了证明MBA-Blast的有效性,作者选取了10000个MBA表达式的数据集对MBA-Blast及目前类似的解决方案进行测试,实验结果表明只有MBA-Blast能够成功化简所有的MBA表达式,且其开销可忽略。
Background
MBA Expression
MBA在计算机科学领域有广泛的应用,如优化、编码、压缩等,常见的MBA表达式:
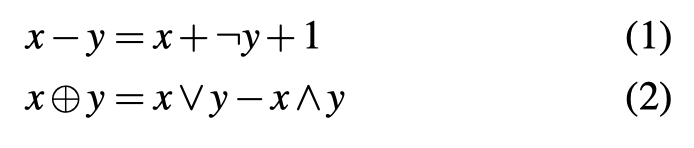
定义:
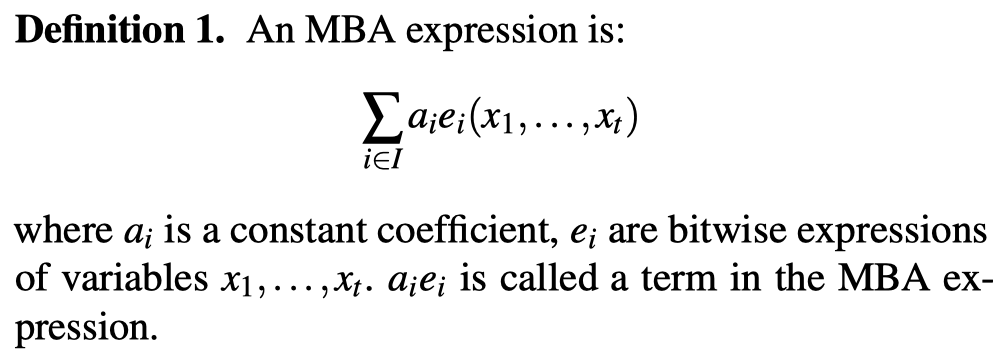
MBA Obfuscation
之前有人证明了:any Boolean function has its non-trivial MBA expression equivalents。为MBA混淆奠定了理论基础。市面上也有诸多开源、闭源的MBA混淆方案。
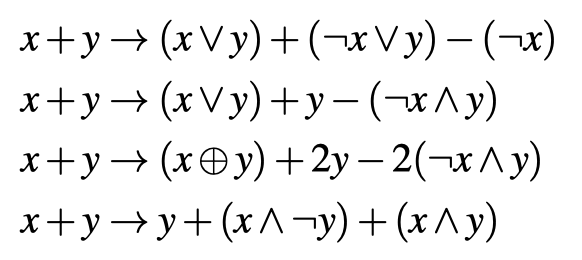
Strength of MBA Obfuscation
Potency、Resilience、Cost、Correctness

Deobfuscation of MBA Expressions
前人尝试了多种去混淆的方式,但都无法通用/效果不佳:符号计算软件(Maple, Wolfram Mathematica, SageMath, and Z3)、LLVM编译时优化、SSPAM等使用的模式匹配、适用于特定MBA模式的代数化简、使用program synthesis生成一个更简单但等价的表达式…
现有工作共有的局限性在于,他们将MBA混淆视为一个黑箱,而没有研究内在的原理。作者还发现缺乏全面的MBA ground truth。
How MBA Obfuscation Works: from One-bit to N-bit
Zhou et al. [24]提出了一种自动化生成MBA等式的方法。以两个布尔变量、五种运算为例:

尽管这只能生成1-bit变量,但Zhou等人证明了该方法对任意长度的整数都适用。
Our Finding: “N-bit to One-bit” Also Holds
作者发现现有的MBA混淆设计实际上是隐含了1-bit和n-bit变量的双向转换。n-bit到1-bit的转换是去除MBA混淆的基础。
作者使用反证法进行了证明,略过。
MBA-Blast
- 将n-bit空间中的表达式En转换为1-bit空间中的E1
- 在1-bit空间中找到E’1使得E1-E’1 = 0
- 将E’1从1-bit空间转换为n-bit空间
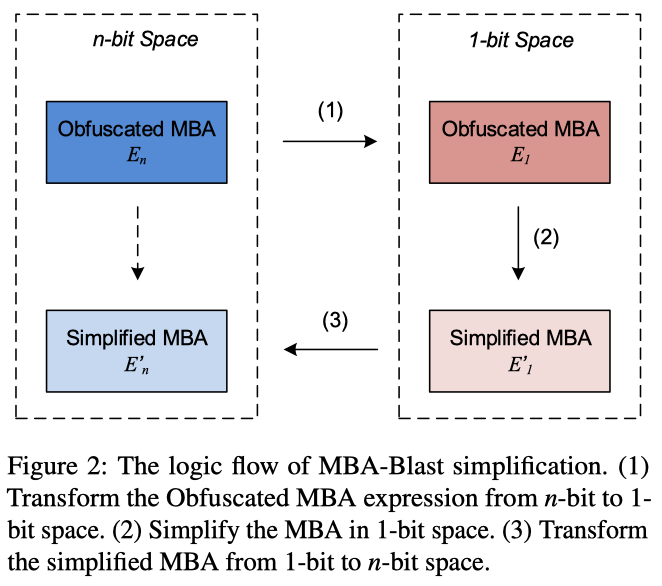
第1、3步已在Section 3 and 4中证明,核心的是第二步,找到一个1-bit化简后的表达式。
$$E_n - E’_n = 0 \Leftrightarrow E_1 - E’_1 = 0
$$
在1-bit空间上化简的优势在于:可以使用真值表来枚举所有可能的值。

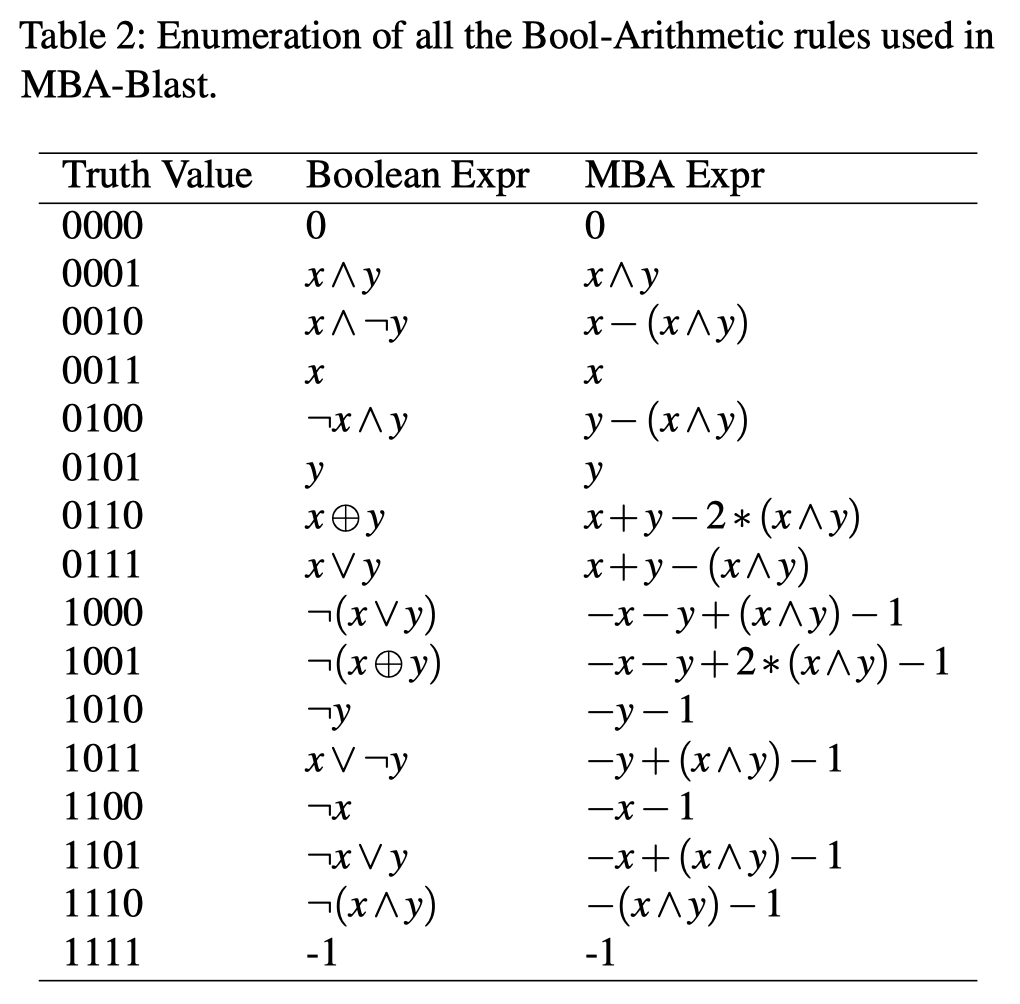
根据Section 3,我们可以由Table 1得到:$x+y − (x∨y) − (x∧y) = 0$,也就意味着$x∨y = x+y−(x∧y)$。通过这种方法我们可以构建两变量的真值表(Table 2)。The truth value of $x∨y$为0111(纵列),通过替换$x∨y$为其他操作得到对应的项。通过这种方式得到的MBA表达式都形如$c_1 x+c_2 y+c_3 (x∧y)−c_4$。
因此可以进行化简:$∑a_i e_i =
∑a_i (c_1i x+c_2i y+c_3i (x∧y)−c_4i )
= C_1 x+C_2 y+C_3 (x∧y)−C_4$
Section 3中的例子:
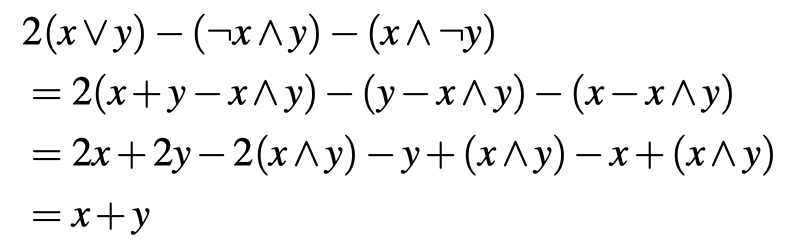
Figure 1中的例子:

Implementation
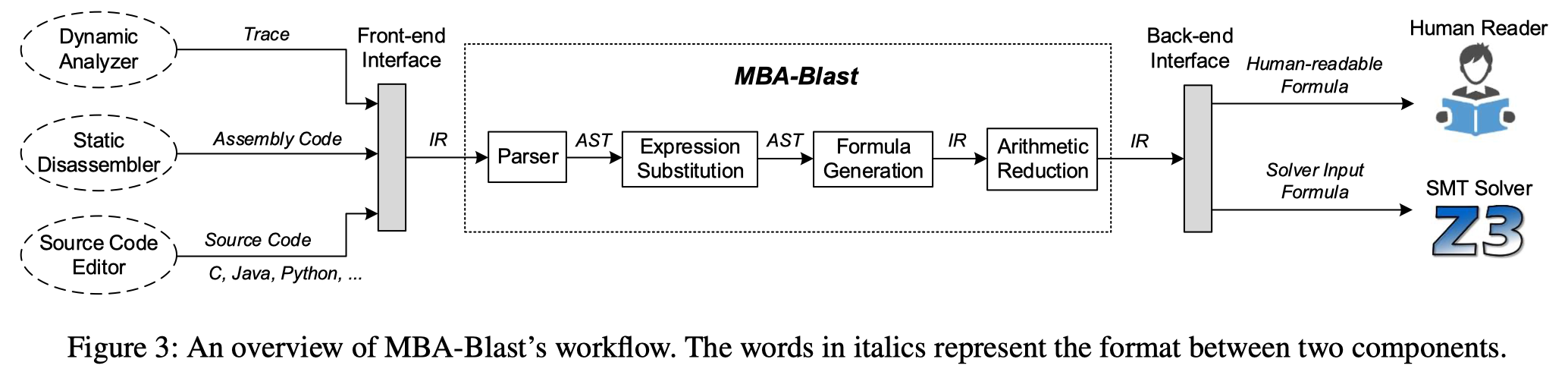
Evaluation
Experimental Setup
dataset 1:

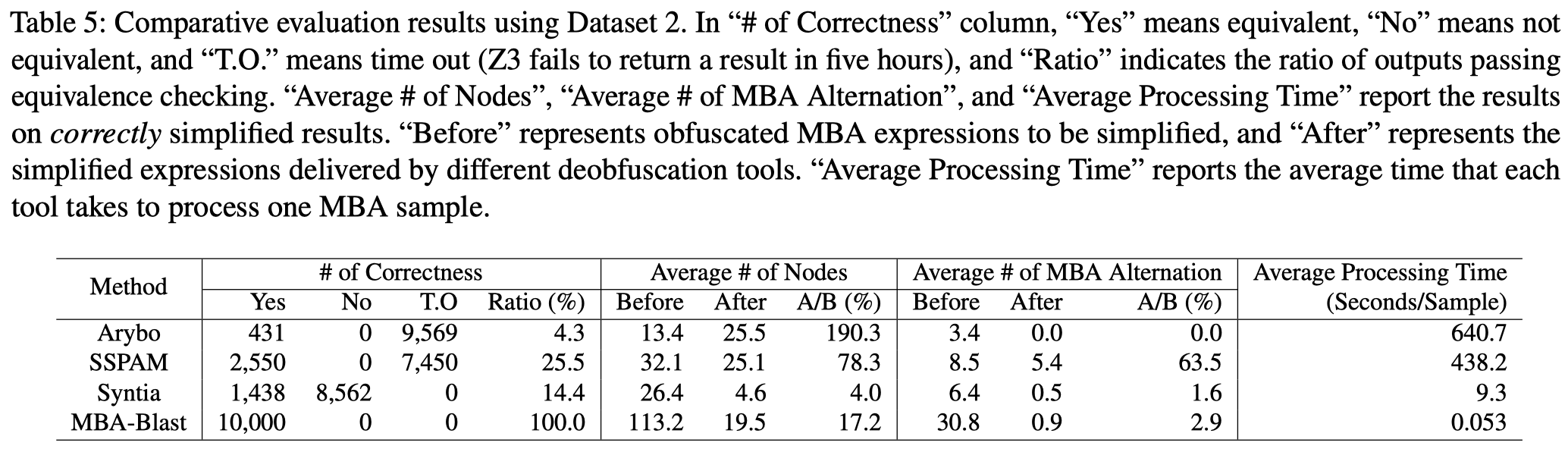
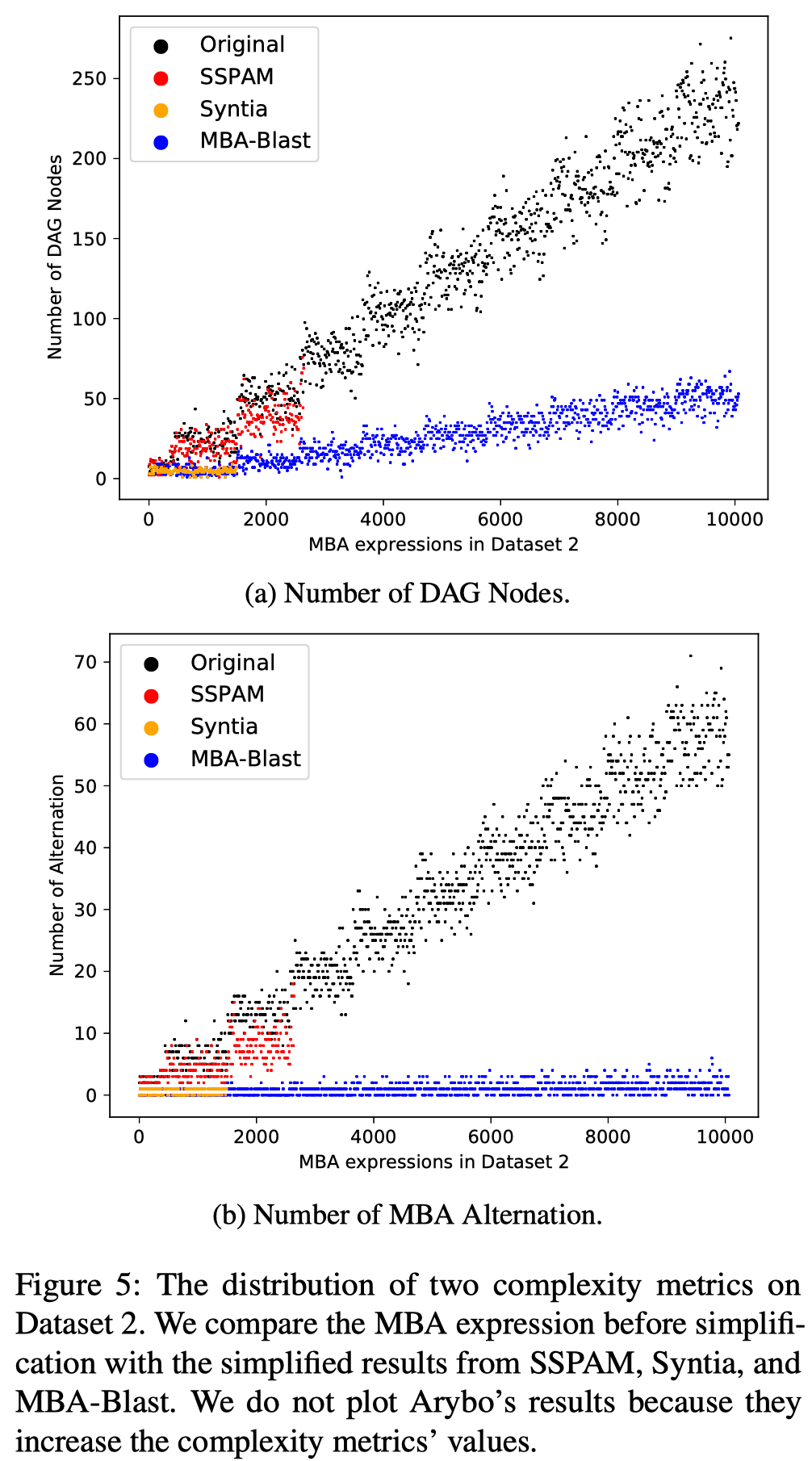
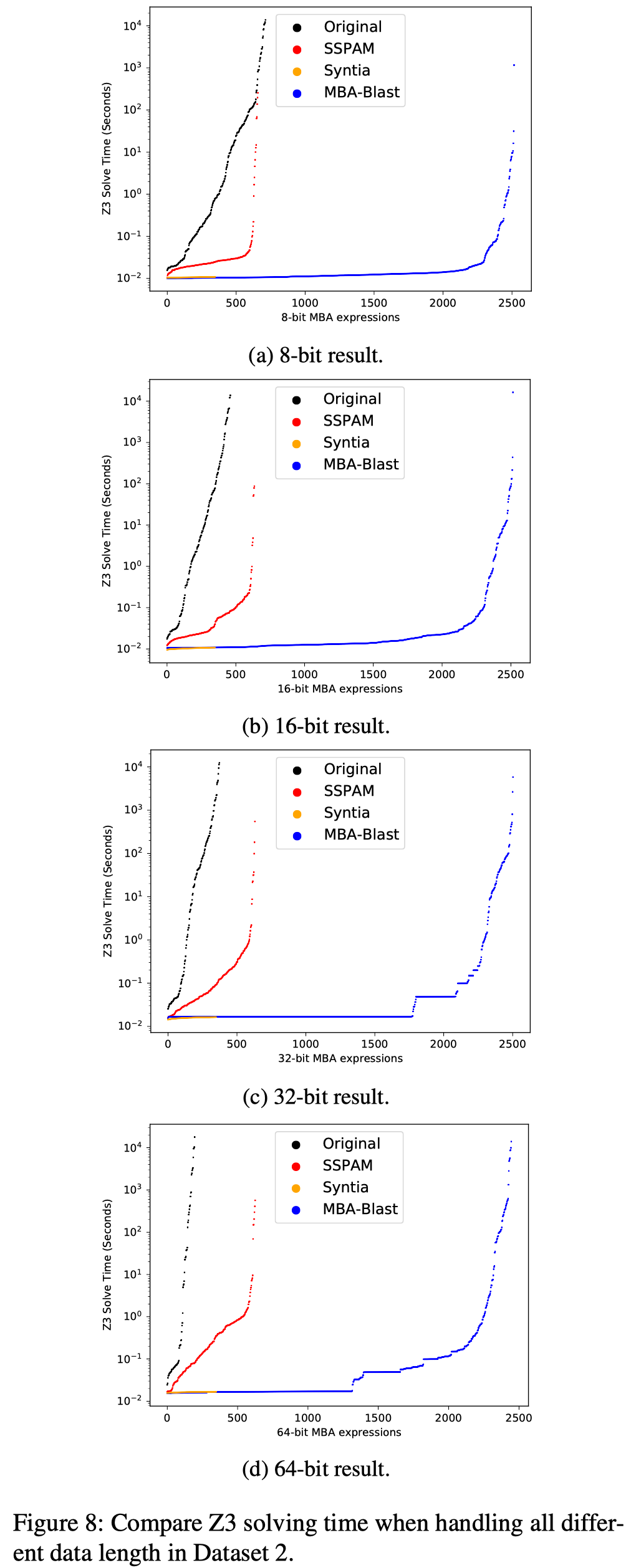
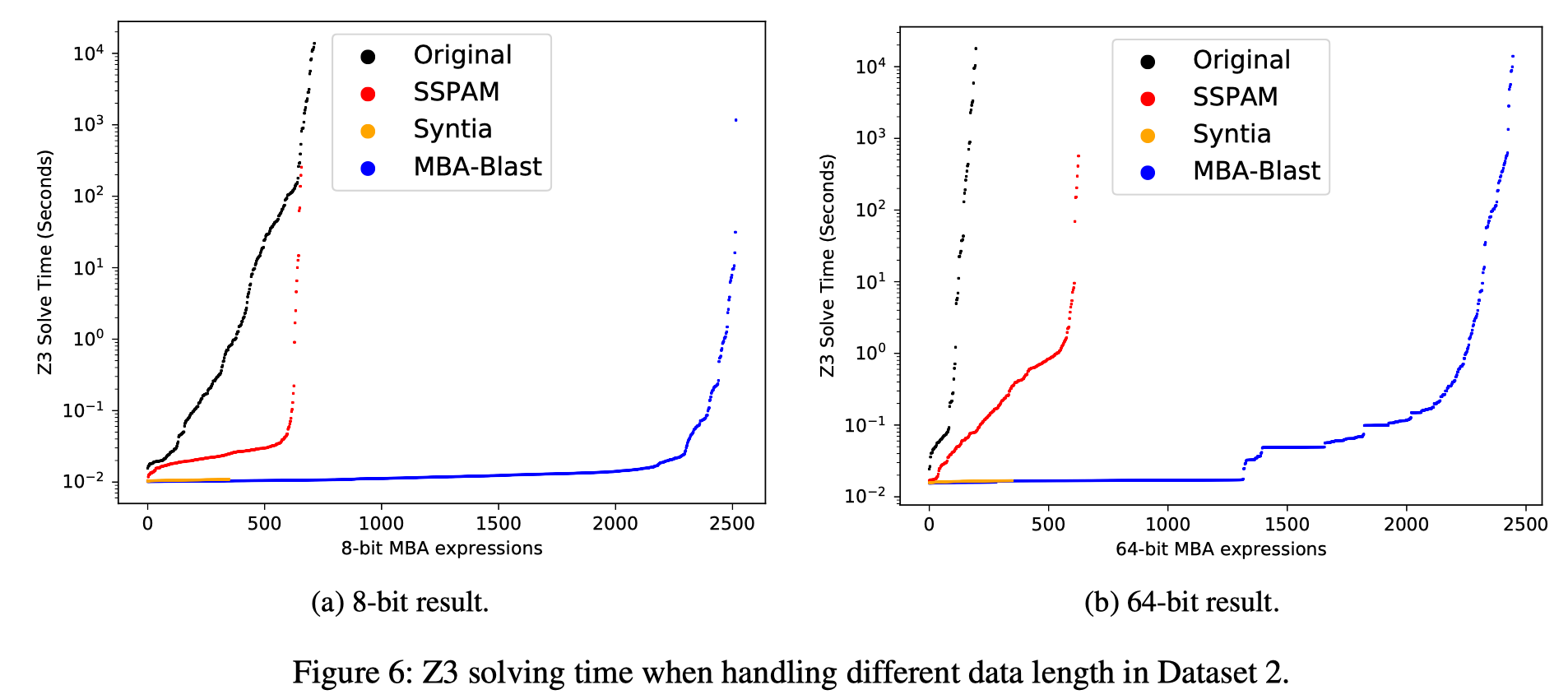
Dataset 2:
10000条MBA表达式,考虑了Length of variables、Number of variables、Number of terms
Peer Tools for Comparison
Arybo [33], SSPAM [34], and Syntia [21]
Dataset 1: Collected MBA Examples
Dataset 2: Comprehensive MBA Dataset
Defeating Tigress MBA Obfuscation
Solving MBA-Powered Opaque Predicates
MBA Usage in Real-World Malware
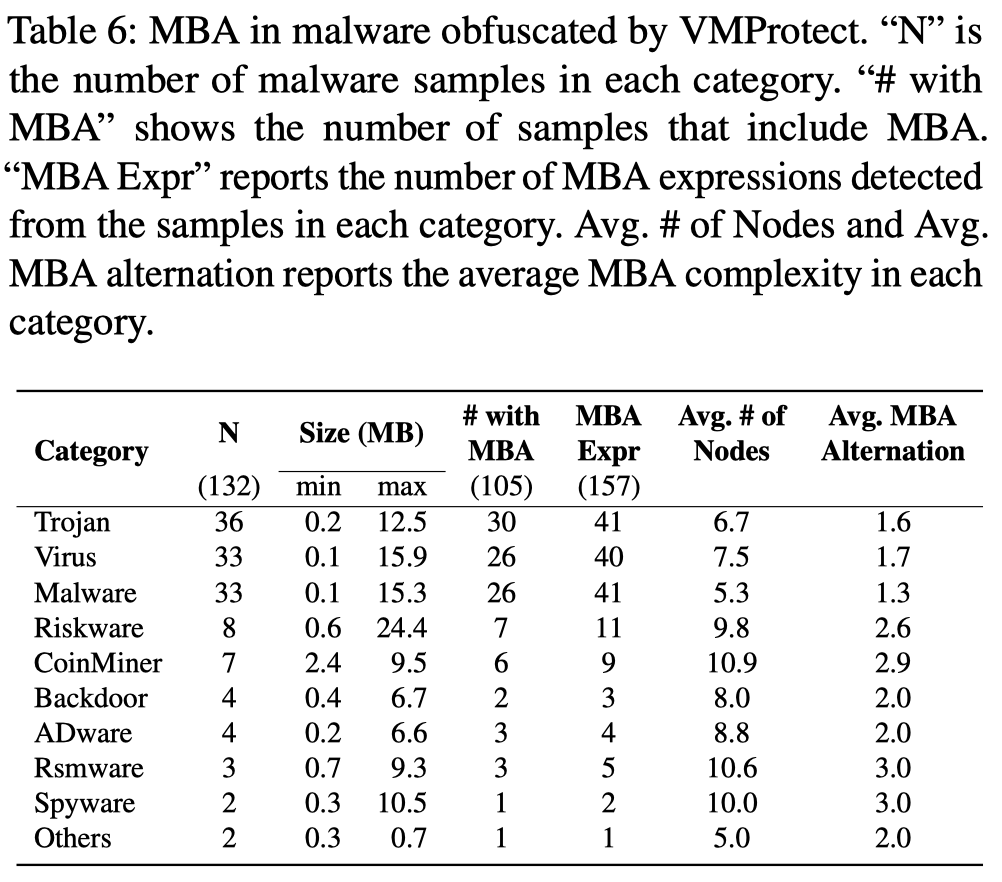

Conclusion
本文提出了一种针对于Mixed BooleanArithmetic (MBA) obfuscation的解混淆方案。作者研究了MBA混淆内在的数学原理,并证明了1-bit和n-bit变量之间双向转换特征。基于这一发现实现了MBA-Blast,将MBA表达式在1-bit空间中进行算术规约。作者通过大规模的MBA实验以及real-world恶意软件研究,证明了MBA-Blast的有效性和通用性。